티스토리 뷰
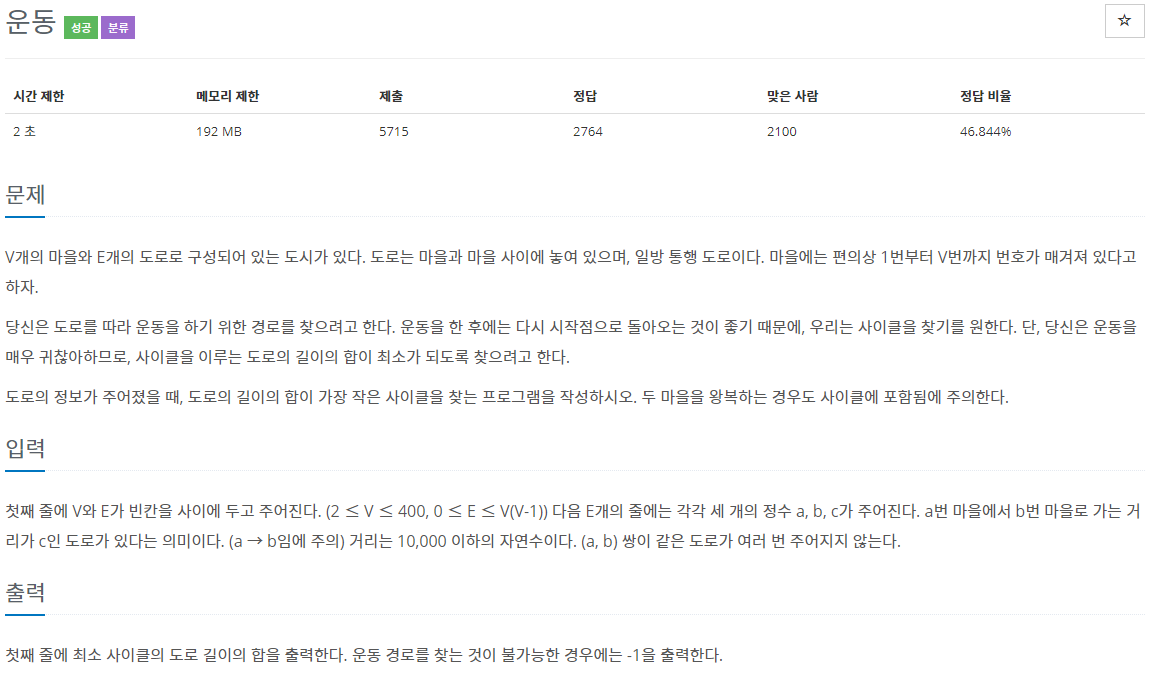
문제를 요약하면 사이클이 있는 경로 중 최단경로를 찾으면 된다.
시작점과 도착점을 특정한 상태에서 최단거리를 구할 수 없으므로, 플로이드-와샬 알고리즘을 통해 모든 노드 간의 최단거리를 구한다.
알고리즘을 수행한 후에 dist[i][j]는 i노드에서 j노드까지의 최단거리가 된다.
문제에서 사이클이 존재해야 한다고 했으므로 dist[i][j]와 dist[j][i]가 모두 존재해야 한다.
즉, 'i번 노드에서 j번노드까지의 최단거리 + j번 노드에서 i번 노드까지의 최단거리' 중 가장 작은값이 정답이 될 것이다.
/*
21.02.05
BOJ : 1956 운동 (https://www.acmicpc.net/problem/1956)
플로이드-와샬 알고리즘
*/
#include <bits/stdc++.h>
using namespace std;
int v, e;
int dist[401][401];
void init() {
for (int i = 1; i <= v; i++) {
for (int j = 1; j <= v; j++) {
dist[i][j] = INT_MAX;
}
}
}
void floyd() {
for (int k = 1; k <= v; k++) {
for (int i = 1; i <= v; i++) {
for (int j = 1; j <= v; j++) {
if (dist[i][j] > dist[i][k] + dist[k][j]) {
if (dist[i][k] == INT_MAX || dist[k][j] == INT_MAX) continue;
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> v >> e;
init();
while (e--) {
int s, e, c;
cin >> s >> e >> c;
dist[s][e] = c;
}
floyd();
int mn = INT_MAX;
for (int i = 1; i <= v; i++) {
for (int j = 1; j <= v; j++) {
if (i == j) continue;
if (dist[i][j] == INT_MAX || dist[j][i] == INT_MAX) continue;
mn = min(mn, dist[i][j] + dist[j][i]);
}
}
cout << (mn == INT_MAX ? -1 : mn);
return 0;
}
'알고리즘 풀이 > 그래프' 카테고리의 다른 글
| BOJ : 1865 웜홀 (0) | 2021.02.03 |
|---|---|
| BOJ : 10282 해킹 (0) | 2021.02.02 |
| BOJ : 1854 K번째 최단경로 찾기 (0) | 2021.02.01 |
| BOJ : 1613 역사 (0) | 2021.01.22 |
| BOJ : 9470 Strahler 순서 (0) | 2021.01.22 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- ReactNative
- nestjs
- 자바스크립트
- 컴퓨터 구조
- 알고리즘
- nest.js
- boj
- typeORM
- BFS
- 시뮬레이션
- 컴퓨터 통신
- java
- 예외처리
- node.js
- 백준
- 그래프
- nodeJS
- 백트래킹
- 세그먼트 트리
- 벨만포드
- dfs
- 재귀
- 자바
- 중앙대학교
- 구현
- Computer Architecture
- 투포인터
- 동적계획법
- 스레드
- 그리디
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
글 보관함
