티스토리 뷰
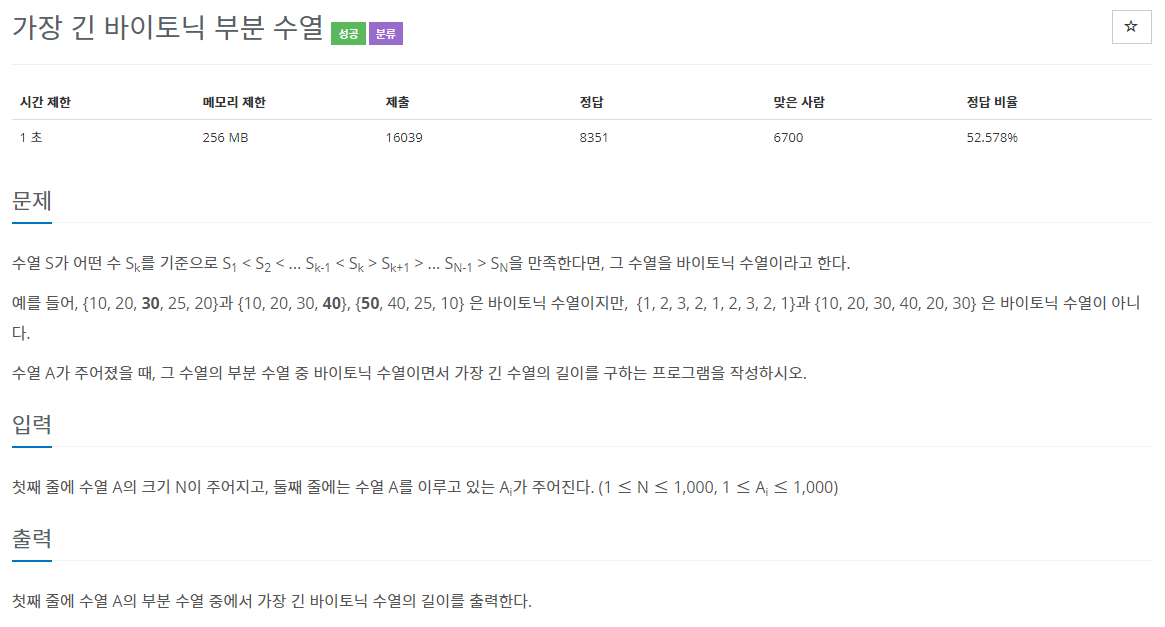
[BOJ 11054(G3) 리뷰]
이 문제는 LIS알고리즘을 통해 풀 수 있다.
다만 기존에는 가장 긴 증가하는 부분 수열의 길이를 출력했다면 이 문제는
"수열 S가 어떤 수 Sk를 기준으로 S1 < S2 < ... Sk-1 < Sk > Sk+1 > ... SN-1 > SN "라는 조건을 만족해야 한다.
{10,20,30,25,20}과 같이 30이라는 수를 기준으로 왼쪽에는 오름차순 정렬이 되있으며 오른쪽은 내림차순이다.
우리는 주어진 수열에서 위 조건을 만족하는 가장 긴 바이토닉 수열의 길이를 찾아야 한다.
만약 {1 5 2 1 4 3 4 5 2 1}라는 데이터가 주어졌다면 이 데이터에서 가장 긴 증가하는 바이토닉 수열은
{1 5 2 1 4 3 4 5 2 1}이 된다. 5를 기준으로 왼쪽은 오름차순, 오른쪽은 내림차순이다.
처음에 이 문제를 어떻게 풀어야할지 고민을 많이 했다.
입력데이터가 1000밖에 안되니 완전탐색으로도 풀릴것 같았다.
그러나 다른접근을 통하여 문제를 해결했다.
우리의 목표는 가장 길이가 긴 바이토닉 수열의 길이를 출력하는 것이다.
이것을 다르게 생각해보면 임의의 기준점을 기준으로 ->방향에서의 길이와 <-방향에서의 길이가 최대가 되어야 한다.
그래서 먼저 왼쪽부터 가장 길이가 긴 증가하는 수열을 찾았다.
{1 5 2 1 4 3 4 5 2 1} 이며 길이는 5이다.
각각의 DP를 나타내어 보면 [1,2,2,1,3,3,4,5,2,1]이다.
그렇기에 [1,2,2,1,3,3,4,5,2,1] 일때 ->방향의 가장 긴 증가하는 부분 수열이 된다.
이제 반대로 <-방향에서 가장 긴 증가하는 부분 수열의 DP값을 계산해 보자.
[1,4,2,1,4,3,3,3,2,1]이다. 가장 큰 값은 4이지만 우리는 임의의 자리에서 앞의 길이와 뒤의 길이가 최대가 되는 위치를 구해야 한다. 각각의 DP값을 정리해보면
->방향 DP값은 [1,2,2,1,3,3,4,5,2,1] 이며
<-방향 DP값은 [1,4,2,1,4,3,3,3,2,1] 이다.
이로서 우리는 각각의 자리에 대해 ->방향에서 가장 긴 길이와 <-방향에서 가장 긴 길이를 구했다.
이제 이 DP값의 합이 가장 큰 곳이 바이토닉 수열에서 기준점의 위치가 될것이며 이때의 길이가 가장 긴 바이토닉 부분 수열의 길이가 될 것이다.
따라서 두개의 DP값을 합하면 [2,6,4,2,7,6,7,8,4,2] 가 되고 가장 큰 값은 8이며 해당 자리가 중복되었으므로 1을 빼주면 가장 긴 바이토닉 부분 수열의 길이를 얻을 수 있다.
나는 가장 길이가 긴 부분 수열1 에서 사용했던 코드를 그대로 사용했다.
다만 뒤에서부터 DP값을 계산해줘야 하므로 reverse함수를 이용하여 배열을 반대로 뒤집고 <-방향의 DP값을 구했다.
#include <bits/stdc++.h>
using namespace std;
int arr[1001];
int dp[1001];
int dp2[1001];
int main(void)
{
int N;
cin >> N;
for (int i = 0; i < N; i++)
{
cin >> arr[i];
dp[i] = 1;
dp2[i] = 1;
}
for (int i = 0; i < N; i++)
{
int temp=0;
for (int j = 0; j < i; j++)
{
if (arr[i] > arr[j])
{
dp[i] = max(dp[i], dp[j]+1);
}
}
}
reverse(arr, arr + N);
for (int i = 0; i < N; i++)
{
int temp = 0;
for (int j = 0; j < i; j++)
{
if (arr[i] > arr[j])
{
dp2[i] = max(dp2[i], dp2[j] + 1);
}
}
}
reverse(dp2, dp2 + N);
int ans = 0;
for (int i = 0; i < N; i++)
{
ans = max(ans, dp[i] + dp2[i]);
}
cout << ans-1;
}

'알고리즘 풀이 > 동적계획법' 카테고리의 다른 글
| BOJ : 1520 내리막 길 (0) | 2020.08.31 |
|---|---|
| BOJ : 11048 이동하기 (0) | 2020.08.28 |
| BOJ : 9465 스티커 (0) | 2020.08.28 |
| BOJ : 1932 정수 삼각형 (0) | 2020.08.28 |
| BOJ : 11055 가장 큰 증가 부분 수열 (0) | 2020.08.26 |
- Total
- Today
- Yesterday
- typeORM
- 자바스크립트
- 자바
- 그리디
- 재귀
- 예외처리
- 동적계획법
- 컴퓨터 통신
- 세그먼트 트리
- 구현
- 알고리즘
- 컴퓨터 구조
- 백트래킹
- Computer Architecture
- nest.js
- java
- 백준
- ReactNative
- nodeJS
- 투포인터
- 중앙대학교
- dfs
- BFS
- node.js
- 스레드
- 그래프
- 시뮬레이션
- boj
- 벨만포드
- nestjs
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
