티스토리 뷰
이 포스트는 「"Computer Organization and Design -The hardware / software interface"
by Patterson and Hennessy, 5th edition, 2013.」을 참고하여 작성했습니다.
CH3. Arithmetic for Computers
인간은 무한대에 대해 생각할 수 있지만 컴퓨터는 항상 한정된 공간의 자원만 사용이 가능하다.
따라서 컴퓨터로 무한대의 수를 표현하는 것은 불가능하다. 한정된 숫자만 표현할 수 있다.
컴퓨터는 한정된 숫자만 표현할 수 있기에 산술 연산을 할 때 Overflow가 발생할 수 있다.
이는 데이터를 저장할 수 있는 Bit를 초과하여 발생하는 현상이다.
예를 들어 단 3bit만 존재한다면 부호가 없다고 가정했을 때 최대 8까지의 숫자를 표현할 수 있다.
그렇기 때문에 만약 7+6이라는 연산을 수행하게 된다면 Overflow가 발생할 것이다.
덧셈 연산에서 오버플로우가 발생하는 경우는 아래와 같다.
- 두 개의 양수를 더했는데 결과가 음수 값이 나옴
- 두 개의 음수를 더했는데 결과가 양수 값이 나옴
뺄셈 연산에서 오버플로우가 발생하는 경우는 아래와 같다.
- 음수-양수의 결과값이 양수이다.
- 양수-음수의 결과값이 음수이다.
위 경우들은 인간이 계산해서는 절대 나올 수 없는 결과지만, 컴퓨터의 한정된 Bit로 인하여 나오는 결과이다.
C언어 같은 경우는 Overflow를 무시하므로 별도의 경고 메시지 등이 출력되지 않는다.
따라서 개발자는 반드시 오버플로에 대해 알고 있어야하며 프로그래밍 시에 이를 주의해야 한다.
반면에 Ada,Fortran같은 경우는 Overflow가 발생하게 되면 인터럽트를 발생시킨다.
Multiplication
컴퓨터에서 곱셈연산이 어떻게 수행되는지 알아보자.
먼저 long-multiplication 접근 방법이다.

위 그림은 인간이 곱셈을 할 때의 과정이다. 컴퓨터도 비슷한 과정을 통해 곱셈 연산을 수행하게 된다.
총 N-bit의 크기라면 N-Step의 과정을 거친다.

32Bit에서의 실제 회로를 그림으로 나타낸 것이다.
64Bit의 레지스터와 64Bit의 ALU가 필요하다.
과정은 아래와 같다.
- Multiplier의 맨 오른쪽 bit를 확인한다.
- bit가 1이면 multiplicand의 값을 Product와 더한다. 0이라면 더하지 않는다.
- 위 과정을 마친후 Multiplier를 right shift 한다.
- Multiplicand를 left shift 한다. (Multiplicand는 64Bit이다)
- 위 과정을 n번 반복 후의 product값이 결과이다.
순서대로 나타내면 아래와 같다.

위 과정을 통해 Multiplication이 수행함을 확인했지만 우리는 32bit에서 64bit의 ALU와 레지스터를 사용해야 함을 알 수 있다. 그래서 나온 방법이 Optimized Multiplier이다.
Optimized Multiplier는 32Bit의 ALU와 레지스터를 사용한다.

Product의 왼쪽 Bit는 덧셈을 위하여 사용하고 오른쪽 Bit는 Multiplier를 담고 있다.
먼저 Product 오른쪽에 있는 Multiplier비트 중 맨 오른쪽의 Bit를 확인한다.
1이면 Product의 왼쪽 Bit에 Multiplicand를 더하고 right shift 한다. 0이라면 그냥 right shift한다.
위 과정을 n번 반복하면 Product의 비트를 통해 결과값을 확인할 수 있다.
곱셈 연산은 n-step의 과정을 거치기에 덧셈 연산보다 느릴 수밖에 없다.
따라서, 반드시 2^n의 곱셈을 할 경우에는 shift연산을 이용하고, 곱셈을 덧셈으로 대체 가능하다면 덧셈 연산을 이용하자.(요즘 컴파일러는 알아서 바꿔주기도 한다.)
느린 곱셈 연산을 극복하기 위해 파이프라인을 이용하여 병렬로 처리할수도 있다.(CH4에 다룸)
MIPS에서는 곱셈연산을 위해 2개의 32Bit 레지스터를 사용한다.(Product에 사용)
HI, LO로 각각 32Bit의 레지스터이다.
Division
컴퓨터가 나눗셈 연산을 어떻게 수행하는지 알아보자.
사람은 나눗셈을 어떻게 할까? 5/2가 있다면 5를 2로 두 번 나누고 나머지가 1이 남는 것을 알 수 있다.
즉, 5=2*2+1이 된다.
Long-division 접근방법도 위와 비슷하다.

5/2에서 5는 dividend가 되고 2는 divisor가 된다. 몫인 2는 quotient가 되며 나머지는 remainder라 한다.
먼저 컴퓨터는 나눗셈을 뺄셈 연산을 통해 수행한다는 것을 기억하자. 예를 들어 5/2가 있다고 하자.
5에서 2를 뺀다. 나머지의 값이 2보다 큰지 확인한다. (나머지 3)
나머지가 2보다 크므로 다시 3에서 2를 뺀다. (나머지 1)
나머지의 값이 2보다 작으므로 과정을 멈춘다. 뺀 횟수가 몫이 되며 남은 값이 나머지가 된다.
컴퓨터에서 나눗셈은 뺄셈을 통해 수행되기에 0으로 나누는 일을 해서는 안된다. 무한루프가 발생하게 된다.
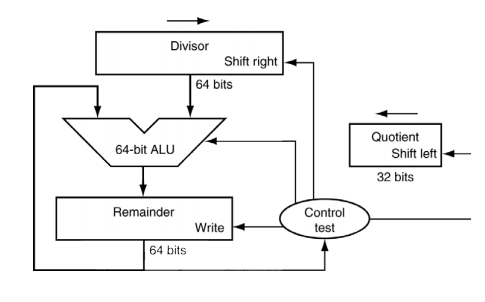
나눗셈 연산에 이용되는 논리회로이다.
Remainder레지스터에 dividend값이 들어있다.
그리고 divisor의 왼쪽 bit에는 divisor의 값이 오른쪽은 0으로 초기화되어있다.
- Remainder-Divisor를 수행한다.
- 결과의 맨 왼쪽 Bit를 확인한다. 0이라면 Quotient에 1을 put 하고 left shift 한다.
- 1이라면 Quotient에 0을 put 하고 left shift 한 후에 다시 Divisor를 더해 원래 값으로 back 한다
- Divisor를 right shift 한다.
- 이 연산을 n번 반복하여 나온 remainder가 나머지가 되며 quotient에 저장된 bit의 맨 오른쪽 bit이 몫이 된다.

Optimized divider 역시 곱셈 연산과 비슷하게 수행된다.
이렇게 컴퓨터에서 곱셈과 나눗셈 연산이 어떻게 수행되는지 알아봤다.
컴퓨터의 2^n 곱셈 연산은 left shift연산을 통해 완벽히 대체가 가능하지만 2^n 나눗셈 연산은 right shift연산을 통해 완벽히 대체가 불가하다. 오직 unsigned interger일 때만 사용이 가능하다.
부호가 있는 비트를 단순히 logical right shift 하게 되면 전혀 엉뚱한 값이 나오게 된다.
그래서 Arithmetic right shift연산을 사용하지만 (부호 비트로 채움) 이 역시 결과가 실제 나눗셈 연산과 다를 수 있다.
예를 들어 -5/4를 계산하면 컴퓨터는 -1 값을 나타내지만(이도 언어마다 결과가 다르다) shift연산을 수행하게 되면 -2의 결과가 나오게 된다.
만약 음수를 나눠야 한다면 dividend와 remainder의 부호를 반드시 같게 하는 규칙을 적용한다.
Lecture Note #8에서 계속..
'Lecture Note > Computer Architecture' 카테고리의 다른 글
| 컴퓨터 구조(CA) Lecture Note #8 (0) | 2020.10.13 |
|---|---|
| 컴퓨터 구조(CA) Lecture Note #6 (0) | 2020.09.28 |
| 컴퓨터 구조(CA) Lecture Note #5 (0) | 2020.09.26 |
| 컴퓨터 구조(CA) Lecture Note #4 (0) | 2020.09.19 |
| 컴퓨터 구조(CA) Lecture Note #3 (0) | 2020.09.12 |
- Total
- Today
- Yesterday
- nestjs
- ReactNative
- dfs
- node.js
- nodeJS
- 구현
- typeORM
- BFS
- boj
- 벨만포드
- 백트래킹
- 자바스크립트
- 예외처리
- nest.js
- 컴퓨터 구조
- 그리디
- 컴퓨터 통신
- 재귀
- 중앙대학교
- 백준
- 시뮬레이션
- 알고리즘
- 투포인터
- Computer Architecture
- 스레드
- 동적계획법
- 세그먼트 트리
- 자바
- java
- 그래프
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
