티스토리 뷰
이 포스트는 「"Computer Organization and Design -The hardware / software interface"
by Patterson and Hennessy, 5th edition, 2013.」을 참고하여 작성했습니다.
floating point
이전 강의에서 정수형 자료의 표현방법과 덧셈, 곱셈 등 연산 방법에 대해 살펴보았다.
그렇다면 실수(Real number)는 어떻게 표현해야할까?
예를 들어 1/3은 0.333333으로 계속 끝이 없는 무한소수이다. 이 값을 어떻게 컴퓨터로 표현할 수 있을까?

위 C 코드의 실행결과는 어떻게 될까? 인간의 관점으로 생각해본다면 0.0부터 시작하여 0.1씩 더하므로 총 10번의 반복문이 실행될 것이라고 생각할 수 있다. 하지만 실제로 위 코드를 실행시켜보면 프로그램이 종료하지 않고 무한반복을 하게 된다.
그 이유는 간단하다. 컴퓨터는 0.1이라는 실수 값을 정확하게 표현할 수 없기 때문이다. 인간의 눈으로 보기에는 0.1이라는 간단한 값이지만 그것이 Binary로 컴퓨터에 저장될 때는 복잡한 과정을 거친다. 그 과정에서 0.1을 존재하는 그대로 완벽하게 표현하는 것은 현재 컴퓨터의 능력으로는 불가능하다.
float point가 컴퓨터에 어떻게 저장되는지 알아보기 전에 "normalized scientific notation"에 대해 알아야 한다.
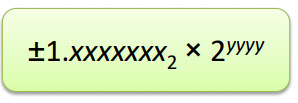
실수는 다양한 방법으로 표현이 가능하다. 1.234 * 10^1이라는 값과 123.4 * 10^-1이라는 값은 같은 결과를 나타낸다.
그렇기 때문에 우리는 컴퓨터와 위와 같은 형태로 실수를 표현하겠다고 약속을 한 것이다. 이는 IEEE Std 754-1985에 의해 정의되었다.

실수가 저장되는 비트의 형태이다. float은 32bit, double은 64bit 자료형이다. 이 강의에서는 float을 기준으로 보겠다.

실제 계산되는 값은 위와 같은 수식을 통하여 계산할 수 있다. 그리고 Fraction에 더해지는 1이라는 값은 숨겨진 값으로써 실제 메모리에 저장되지는 않지만 컴퓨터는 1이 더해진다고 "가정"하고 작업을 수행한다.
다음 Exponent 필드는 2의 지수승이 결정되는 곳이다. 이때 실제 exponent비트에 저장되는 값과 실제로 계산에 사용되는 actual exponent값은 다르다. 즉, exponent는 actual exponent + bias로 계산된다.
float에서의 bias는 127이며 double에서의 bias 1023이 된다.
fraction 필드는 1과 더해지는 소수점 부분을 나타내며 Fraction의 Bit가 전부 1일 때 1과 근사한 값이 된다.
따라서 우리는 위 규칙을 이용하여 실수가 주어졌을 때 Bit로, Bit가 주어졌을때 실수로 번역하는 방법을 알아야 한다.
컴퓨터는 단지 이진수로 된 Bit만을 저장한다. 따라서 저장된 Bit들을 어떻게 읽냐에 따라 결과는 매우 다르게 나타날 수 있다. 예를 들어 00001010이라는 값을 unsigned int로 읽게 되면 10이라는 값이 될것이다. 그러나 이를 float자료형으로 읽게되면 10이라는 값이 나오지 않는다.
따라서 int a=5와 float b=5.0이라는 값은 5라는 값을 동일하게 저장하고 있지만 실제 메모리에 저장되는 Bit의 형태는 다르다. 따라서 Bit자체로는 우리가 그 Bit의 의미를 파악할 수 없다는 점을 반드시 기억해야 한다.
Precision Range
위에서 우리는 실수를 표현할 때 Hidden bit를 통해 1이라는 값을 있다고 가정했다.
그렇기에 항상 1+. xxx꼴이기에 0을 표현할 수가 없다. 따라서 0을 표현하기 위한 약속이 있다.
exponent가 all zero이고 frcation이 all zero이면 그것은 0으로서 약속한다.
exponent가 all one이고 fraction이 all zero라면 그것은 무한대(infinity)로서 약속한다.
exponent가 all one이고 fraction이 0이 아니라면 그것은 Not a number이며
exponent가 all zero이고 fraction이 값을 모른다면 이것은 denormal number이다.
float자료형은 int형에 비해 매우 큰 값을 표현할 수 있다. 10진수로 최대 3.4*10^38의 수까지 표현할 수 있다. 엄청나게 큰 숫자이다. 숫자는 지수승에 비례하여 커지지만 frcation에는 한계가 있으므로 값이 커질수록 정확도는 점차 낮아지게 된다.
따라서 float에는 유효숫자라는 것이 존재한다. float형의 경우 소수점 여섯째짜리, double형은 16째짜리까지 유효숫자로 나타낼 수 있다.
또한 위에 말한 denormal number는 매우 작은 숫자를 표현하기 위한 방법으로, hidden bit에 1이 들어가는 것이 아닌 0이 들어가 0을 더하므로 매우 작은 값을 표현할 수 있다. exponenet가 all zero이고 fraction이 0이 아니라면 이에 해당한다.
Floating-Point Addition
부동소수점의 덧셈 연산에 대해 알아보자.
과정은 아래와 같다.
- 두 숫자 간의 지수를 맞춰야 한다. 지수가 작은 것을 지수가 큰 것에 맞춰준다.
- 지수를 맞췄으니 더해준다.
- 더해준 결과를 normalize 해준다.
- 반올림하거나 renormalize 한다.
곱셈 연산은 아래와 같다.
- 지수끼리 더해준다.
- Significands를 곱한다.
- 결과를 normalize 한다.
- round and renormalize
- sign을 결정한다.
이때 지수끼리 더할 땐 반드시 actual exponent를 더해줘야 한다.
MIPS에서의 부동소수점 연산은 보통 FP 연산을 위한 Hardware를 통해 이루어진다.
부동소수점 연산은 다른 연산에 비해 복잡하고 많은 사이클이 필요하기에 매우 느리다.
FP 연산 하드웨어는 덧셈, 뺄셈, 곱셈, 나눗셈, reciprocal, square-root, conversion 등을 지원한다.
MIPS에는 FP 연산을 위한 레지스터도 따로 존재한다. 총 32개의 레지스터이며 double형의 경우 레지스터를 2개씩 사용한다. FP 연산은 오직 FP레지스터를 통해서만 이루어진다.
Accurate Arithmetic
부동소수점의 정확한 연산을 위해 IEEE Std 754 rounding control규정이 존재한다.
guard, round, stick 3개의 비트를 이용하여 반올림의 정확성을 높인다.
예를 들어 숫자 3개까지 반올림을 한다면 그다음 숫자가 guard, 그 다음 숫자가 round가 된다.
sticky는 guard와 round와 달리 조금 특별하다. round뒤 숫자가 모두 0이라면 sticky는 0이며 모두 0이 아니라면 sticky는 1이 된다.
또한 rounding mode도 존재한다. 종류에는 up, down, truncate, nearest even, away from 0등이 있다. 이는 사용자가 정하여 사용한다. 데이터가 클수록 반올림에 의하여 그 결과가 달라질 수 있다. rounding option은 데이터의 사용목적에 따라 바뀐다는 점을 기억해야 한다.
부동소수점으로는 매우 큰 숫자를 표현할 수 있다. 그러나 부동소수점을 컴퓨터가 표현하는 특징 때문에 생기는 오류가 몇 가지 있다.
(1.5 * 10^32 +1) - 1.5*10^32의 결과는 무엇일까? 1이라고 생각하겠지만 아니다. 답은 0이다.
그러나 (1.5 * 10^32 - 1.5 * 10^32) +1의 결과는 올바르게 1이 나온다.
두 개가 같은 수식임에도 불구하고 답이 다르게 나오는 이유는 컴퓨터는 매우 큰 숫자와 매우 작은 숫자를 함께 처리할 수 없기 때문이다. 개발을 할 때 매우 큰 숫자와 매우 작은 숫자를 함께 사용하는 것은 지양해야 한다.
'Lecture Note > Computer Architecture' 카테고리의 다른 글
| 컴퓨터 구조(CA) Lecture Note #7 (0) | 2020.10.05 |
|---|---|
| 컴퓨터 구조(CA) Lecture Note #6 (0) | 2020.09.28 |
| 컴퓨터 구조(CA) Lecture Note #5 (0) | 2020.09.26 |
| 컴퓨터 구조(CA) Lecture Note #4 (0) | 2020.09.19 |
| 컴퓨터 구조(CA) Lecture Note #3 (0) | 2020.09.12 |
- Total
- Today
- Yesterday
- 컴퓨터 구조
- typeORM
- 재귀
- BFS
- 시뮬레이션
- 구현
- 백준
- java
- 투포인터
- 스레드
- 동적계획법
- 예외처리
- dfs
- 중앙대학교
- 세그먼트 트리
- 그래프
- nest.js
- Computer Architecture
- 자바스크립트
- 알고리즘
- 벨만포드
- 컴퓨터 통신
- 자바
- ReactNative
- boj
- 백트래킹
- nestjs
- 그리디
- nodeJS
- node.js
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
